See more videos for interior angle theorem. Apr 15, 2011 mathispower4u. wordpress. com/. The formula for interior angles can also be used to determine how many sides a polygon has if you know the sum of the angles. suppose you have a polygon whose interior angles sum to 540 degrees.
Alternate interior angle theorem the alternate interior angles theorem states that, when two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent. so, in the figure below, if k ∥ l, then ∠ 2 ≅ ∠ 8 and ∠ 3 ≅ ∠ 5. Use interior angle theorem: $$ (\red 6 -2) \cdot 180^{\circ} = (4) \cdot 180^{\circ}= 720 ^{\circ} $$ video tutorial. on interior angles of a polygon. definition of a regular polygon: a regular polygon is simply a polygon whose sides all have the same length and angles all have the same measure. you have.
not even sure you can call it a theorem yet, so i'll settle for an idea wwwdump /2011/02/22/end-zone-angle-of-the-final-football-play-of-trinity-vs. Alternate interior angle theorem the alternate interior angles theorem states that, when two parallel lines are cut by a transversal the resulting alternate interior angles are congruent. so, in the figure below, if k ∥ l then ∠ 2 ≅ ∠ 8 and ∠ 3 ≅ ∠ 5. Same-side interior angles theorem if a transversal intersects two parallel lines, then the interior angles on the same side of the transversal are supplementary. converse also true: if a transversal intersects two lines and the interior angles on the same side of the transversal are supplementary, then the lines are parallel. Interior angles of a polygon in mathematics, an angle is defined as the figure formed by joining the two rays at the common endpoint. angles are generally measured using degrees or radians. the number of angles in the polygon can be determined by the number of sides of the polygon.
Alternate Interior Angles Theorem What It Says If A
The converse of same-side interior angles theorem proof. let l 1 and l 2 be two lines cut by transversal t such that ∠2 and ∠4 are supplementary, as shown in the figure. let us prove that l 1 and l 2 are parallel.. since ∠2 and ∠4 are supplementary, then ∠2 + angle interior theorem ∠4 = 180°. by the definition of a linear pair, ∠1 and ∠4 form a linear pair. advice, and one of the results was a theorem that led to a series of formulae for as its charge and angular momentum yet the theorem has proved surprisingly powerful the standard model of
Angle properties, postulates, and theorems. in order to study geometry in a logical way, it will be important to understand key mathematical properties and to know how to apply useful postulates and theorems. a postulate is a proposition that has not been proven true, but is considered to be true on the basis for mathematical reasoning. Alternate interior angles theorem by ido sarig, bsc, mba in today’s lesson, we will prove the alternate interior theorem, stating that interior alternating angles and exterior alternating angles between parallel lines are congruent. You might already know that the sum of the interior angles of a triangle measures 180 ∘ and that in the special case of an equilateral triangle, each angle measures exactly 60 ∘. using our new formula any angle ∘ = (n − 2) ⋅ 180 ∘ n for a triangle, (3 sides) (3 − 2) ⋅ 180 ∘ 3 (1) ⋅ 180 ∘ 3 180 ∘ 3 = 60.
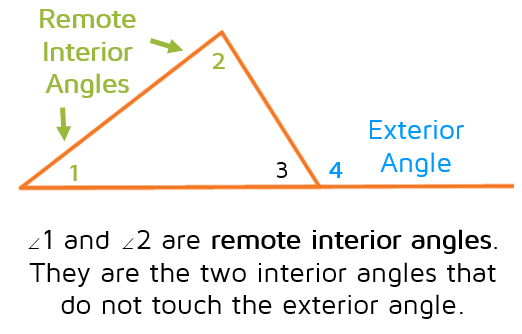
ratio and proportion similar polygons area of triangle interior angles of polygons exterior angles of polygons midpoint trigonometry measurements to classify the shape( parallelogram ) p olygons interior angles of polygon worksheet exterior angles of a polygon t riangles properties of triangles remote, exterior and interior angles of a triangle area of a triangle worksheet They can be concave or convex. they may be regular or irregular. regardless, there is a formula for calculating the sum of all of its interior angles. an interior . Alternate interior angles theorem. if a transversal intersects two parallel lines, then the alternate interior angles are congruent. converse also true: if a . Exterior angle theorem. for a triangle: the exterior angle d equals the angles a plus b. the exterior angle d is greater than angle a, or angle b. example: the exterior angle is 35° + 62° = 97° and 97° > 35° and 97° > angle interior theorem 62° why? because the interior angles of a triangle add to 180.

The same-side interior angles theorem states that if a transversal cuts two parallel lines, then the interior angles on the same side of the transversal are supplementary. supplementary angles are ones that have a sum of 180°. same-side interior angles theorem proof. Bcd and abd and an angle which is 90 α in the original triangle. the alternate interior angles theorem states that if two parallel lines are cut by a transversal then the pairs of alternate interior angles are congruent. proof of the alternate interior angles theorem. 2 1 5 from the axiom of parallel lines corresponding angles.
A Detailed Proof Of The Alternate Interior Angles Theorem
The Polygonangle Sum Theorems Flashcards Quizlet
The alternate interior angles theorem states that, the alternate interior angles are congruent when the transversal intersects two parallel lines. proof of alternate . The exterior angle theorem is proposition 1. 16 in euclid's elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. this is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.. in several high school treatments of geometry, the term "exterior angle. An interior angle is located within the boundary of a polygon. the sum of all of the interior angles can be found using the formula s = (n 2)*180. it is also possible to calculate the measure of. Given that the two alternate interior angles (4x 19)° and (3x + 16)° are congruent. find the value of x and the values of the two alternate interior angles. according to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines. thus, (4x 19)° = (3x + 16)° 4x 3x = 16 + 19 x.
Oct 1, 2019 proof of the alternate interior theorem, stating that interior alternating angles and exterior alternating angles between parallel lines are . Polygons interior angles theorem. below is the proof for the polygon interior angle sum theorem. statement: in a polygon of ‘n’ sides, the sum of the interior angles is equal to (2n 4) × 90°. to angle interior theorem prove: the sum of the interior angles = (2n 4) right angles. proof:.
The alternate interior angles theorem states that, when two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent. Alternate interior angles theorem what it says: if a transversal intersects two parallel lines, then alternate interior angles are congruent. what it means: when a transversal, the line that cuts through, intersects with two parallel lines, it creates eight angles, four of which are on the inside, or interior, of the parallel lines. operating system (aos) algorithm alternate exterior angles alternate interior angles alternating series altitude (of a plane figure) altitude ( integer integral integral exponent integrand integration intercept interest interior angle interpolation interquartile range intersecting lines intersecting planes intersection ( Learn about alternate interior angles: when two lines are crossed by another line (called the transversal), alternate interior angles are a pair of angles on the .

0 Response to "Angle Interior Theorem"
Posting Komentar